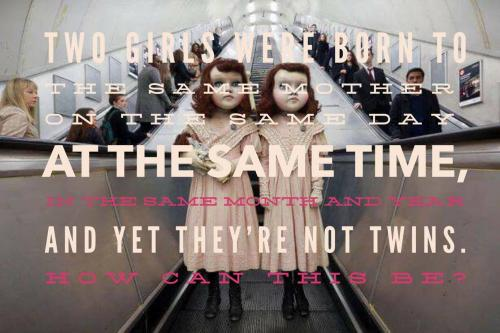Going To Heaven Riddle
Stephen died of heart attack. His soul was received in heaven. He was astonished to find himself as young as he had been in his young adult age. He looked around and there were thousands of young and naked people. His eyes searched to find someone familiar and suddenly he noticed Adam and Eve.
How did Stephen recognize them?
How did Stephen recognize them?
Hint:
Adam and Eve were the only people without navel. As they were not born out of a mother, they never had umbilical cords and thus never had navels. Did you answer this riddle correctly?
YES NO
YES NO
A Couple Of Cannibals Riddle
Michelangelo is being chased by a couple of cannibals who will kill him as soon as they get a hold of him. The only way to get rid of them is crossing the river bridge made of ropes and cut it on reaching the other end. He have found two diamonds in the woods each weighing 8 lbs. The rope is weak and can only accommodate a weight of 150 lbs. He weighs 140 lbs. Still he manages to cross the bridge and get rid of the cannibals with the diamonds without taking off any kind of clothing.
How?
How?
Hint:
Michelangelo juggles the diamonds across while crossing the bridge. Did you answer this riddle correctly?
YES NO
YES NO
The Robbery On The Third Floor Riddle
My wife and I took a much-needed holiday in England. It's a long flight from New York to London. We checked into a nice hotel. After a long day of sightseeing we just collapsed into bed. Just a few minutes ago, we were woken up by some noises outside. I looked out the window and the police were everywhere. They yelled up to me that there was a robbery and a murderer on the second floor. I'm on the third floor, and I can see and I can see that the cops have the stairs and elevators locked down. The murderer can't get up to our floor, so we're in no danger. My wife and I are tired, so we're going back to bed. I really hope they catch the guy.
Why did the police yell to the guy if he was on the 3rd floor?
Why did the police yell to the guy if he was on the 3rd floor?
Hint:
America and England have different ways of numbering floors. In America, it goes 1st floor, 2nd floor, 3rd floor. In England, it goes ground floor, 1st floor, 2nd floor. Did you answer this riddle correctly?
YES NO
YES NO
Making Ten Riddle
Hint:
Yes it is possible in Roman Numerals. In Roman Numerals,
9 = IX
10 = X
11 = XI
Thus by removing one from 9, you are getting 10 and by removing one from 11, you are getting 10 again. Did you answer this riddle correctly?
YES NO
9 = IX
10 = X
11 = XI
Thus by removing one from 9, you are getting 10 and by removing one from 11, you are getting 10 again. Did you answer this riddle correctly?
YES NO
The King And The Kingdom Riddle
Once there lived a king who did not allow anybody to leave the kingdom and any foreigners in his kingdom. There was only one bridge that connected his empire with the outer world. A guard who was a sharpshooter was specially assigned for a lookout on the bridge. According to the orders, anyone moving outside should be killed and anyone coming to his kingdom should be sent back. To take rest, the guard used to sit inside his hut for 5 minutes and return back on the lookout. The bridge took a minimum of 8 minutes to pass.
Even then, a woman was able to escape the kingdom without incurring any kind of harm to the guard.
How ?
Even then, a woman was able to escape the kingdom without incurring any kind of harm to the guard.
How ?
Hint:
The woman started walking across the bridge when the guard was inside the hut. She walked all the time he was inside (5 minutes) and then turned and moved back towards the kingdom. On approaching the kingdom he was asked for papers and since she did not have any, she was sent back. Did you answer this riddle correctly?
YES NO
YES NO
The Homicide Team Riddle
A homicide team enters a crime scene where a dead body of a fat old man lies there on the floor with blood oozing out of his head. The victim is holding a gun and a tape recorder lies there by his side. One of the detective picks up the recorder and plays it "I am tired of this life and hence I have decided to relieve myself from the worldly pains". A gunshot follows the message.
The teams starts investigating a murder investigation.
Why?
The teams starts investigating a murder investigation.
Why?
Hint:
If the man killed himself, he would not have been able to rewind the cassette. Thus it is clear someone else killed him. Did you answer this riddle correctly?
YES NO
YES NO
Making Faces Riddle
When asked what he does all day, a man answered that he sits and makes faces. What does he really mean?
Hint:
Twins Riddle
Hint:
Post Your Mind Boggling Questions Below
Can you come up with a cool, funny or clever Mind Boggling Questions of your own? Post it below (without the answer) to see if you can stump our users.