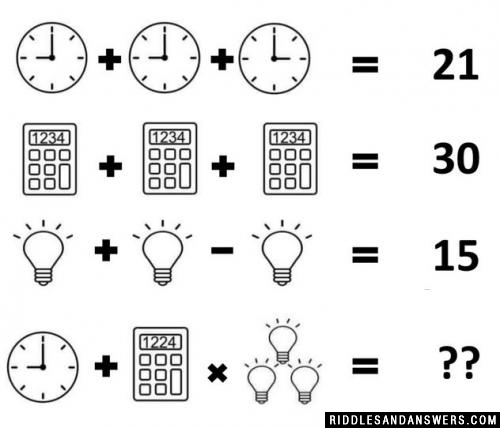Fun Facts (Hints)
Hard riddles are universal, and continue to leave a lasting impression on many different cultures across the globe. Here are some interesting facts:
The mere definition of what a riddle is, is something that has drawn a large amount of debate between scholars for centuries.
Complex riddles have been used since ancient times, and extensively in ancient/medieval literature.
There is only one riddle in the Bible appearing in the book of Judges. It is known as "Samson's riddle."
Charades is a popular contemporary game created with the use of riddle.
In author J. R. R. Tolkien's 'The Hobbit' Bilbo Baggins is given a challenging riddle by Gollum, and his life was dependent upon getting the correct answer.
Trending Tags
Feel free to use content on this page for your website or blog, we only ask that you reference content back to us. Use the following code to link this page:
Search Suggestions
Trouble finding challenging? Here are some search terms related to difficult to try browsing:
hard tough incredible riddles some hard riddles advanced riddles tough riddles with answers really hard riddles with answers very difficult riddles complex riddles extremely hard riddles short hard riddles challenging riddles tough riddles really hard riddles riddles hard difficult riddles
Terms · Privacy · Contact
Riddles and Answers © 2023
Really Hard & Short Complex Riddles To Challenge You
While some hard riddles are meant for mastering instantly, these are the best of the best and more than likely will not be able to be answered promptly.
Whether you are an exceptional thinker who is ready to take on one of the greatest advanced riddles collections known to man or whether you're a teacher that is just looking for some really hard riddles with answers to give out to students, at Riddles and Answers we find the most complex riddles known to man, daily.
Remember before starting that these brain teasers are very tough riddles with answers readily available. If you find yourself stuck on one problem for too long, it's ok to move on to the next one. Just be sure to attempt these challenging riddles every day to help keep your brain functioning at a high level.
4 Prisoner Hat Riddle
Now one of the man needs to call out the color of his hat else they all die in 10 mins. Which man will callout the color of his hat correctly and why?
Hint:
Answer is Man number 2.
Lets start by eliminating men. Man number 4 is at the other end of opaque wall facing other side. There is no way he can see any men or the color of their hat. So he is eliminated. Now man no 3 also cannot see anyone else - he cannot look back and he cannot see beyond wall. So he is eliminated too. Now man number 1 knows the color of man 2 and 3. Now lets say they (2 and 3) were wearing same color hat then man no 1 would know the color of his hat since there are 2 white and 2 black hat. But he keeps mum which means man 2 and 3 are wearing different hat. S0 man number 2 waits for sometime if he does not hear man 1 calling out that means man 2 and 3 are wearing different color hats. Since man 2 knows the color of hat wore by man 3 he know the color of his hat and calls it out. Did you answer this riddle correctly?
YES NO
Lets start by eliminating men. Man number 4 is at the other end of opaque wall facing other side. There is no way he can see any men or the color of their hat. So he is eliminated. Now man no 3 also cannot see anyone else - he cannot look back and he cannot see beyond wall. So he is eliminated too. Now man number 1 knows the color of man 2 and 3. Now lets say they (2 and 3) were wearing same color hat then man no 1 would know the color of his hat since there are 2 white and 2 black hat. But he keeps mum which means man 2 and 3 are wearing different hat. S0 man number 2 waits for sometime if he does not hear man 1 calling out that means man 2 and 3 are wearing different color hats. Since man 2 knows the color of hat wore by man 3 he know the color of his hat and calls it out. Did you answer this riddle correctly?
YES NO
A Man Walks 1 Mile South Riddle
Hint:
He started his journey at the north pole he would end at where he started. At the north pole here is no east or west only south. Once he walks a mile south he would have east and west as well as north and south. Granted north would only consist of 1 mile. Walking a mile north would put him back at the north pole which is a single point. Did you answer this riddle correctly?
YES NO
YES NO
Lambs Goats Turkeys Scottish Field Riddle
You're standing in a Scottish field with green as far as the eye can see and you're standing alone. You check left, you check right and there's nobody anywhere. Out of the horizon the farthest distance away, comes three lambs. They come up to you and say hello. The first one says "My names Marley!", the second one says "My names Barley!", and the third one says "My names Richard!"
You say hello to each and then they go "baaah" and go right back to where they came from. On your left you see three goats approach you from the horizon. "Hello! My names Billy!", My names Jilly!", "My names Willie!" You say hello to each and then they go "baaah" and go back to where they came. On your right you see three turkeys approach you from the horizon. "Hello! My names Veronica!", "My names Maisel!", "My names Brittney!"
You reply hello to each and then they go "baaah" and go back to where they came. All is silent and then you start thinking whos gonna come up behind me? So you turn around.
What three animals approach from behind you and what are their names?
You say hello to each and then they go "baaah" and go right back to where they came from. On your left you see three goats approach you from the horizon. "Hello! My names Billy!", My names Jilly!", "My names Willie!" You say hello to each and then they go "baaah" and go back to where they came. On your right you see three turkeys approach you from the horizon. "Hello! My names Veronica!", "My names Maisel!", "My names Brittney!"
You reply hello to each and then they go "baaah" and go back to where they came. All is silent and then you start thinking whos gonna come up behind me? So you turn around.
What three animals approach from behind you and what are their names?
Hint:
A Girl Has Many Brothers And Sisters Riddle
Hint: Be sure to count the sisters and brothers in total and in terms of their own number of siblings.
4 daughters (sisters) and 3 sons (brothers)
A girl has as many brothers as sisters : If one of the daughters count her siblings, she would count - 3 sisters (3 remaining daughters in the family) and her 3 brothers (3 Sons in the family). So, it makes the statement true that the girl has as many brothers as sisters.
Each brother has only half as many brothers as sisters. This means, when one of the sons count his siblings, it would be 2 brothers (remaining 2 sons of the family) and 4 sisters (All 4 daughters in the family). 2 is the half of 4. It agrees to the condition that
each brother has only half as many brothers as sisters.
Therefore the answer is :
The family has 4 daughters (sisters) and 3 sons (brothers). Did you answer this riddle correctly?
YES NO
A girl has as many brothers as sisters : If one of the daughters count her siblings, she would count - 3 sisters (3 remaining daughters in the family) and her 3 brothers (3 Sons in the family). So, it makes the statement true that the girl has as many brothers as sisters.
Each brother has only half as many brothers as sisters. This means, when one of the sons count his siblings, it would be 2 brothers (remaining 2 sons of the family) and 4 sisters (All 4 daughters in the family). 2 is the half of 4. It agrees to the condition that
each brother has only half as many brothers as sisters.
Therefore the answer is :
The family has 4 daughters (sisters) and 3 sons (brothers). Did you answer this riddle correctly?
YES NO
What Remains When The Roads Are Gone Riddle
Hint:
Let's take a look at the explanation of the riddle.
As per the total laps in the race are 50 and the driver has completed 12 1/2 laps. This means, we have to subtract 12 1/2 from the total 50 laps. This equal to 37 1/2 or 37.5
50 - 12 1/2 = 37 1/2 or 37.5
Now, we need to calculate the fractional part of the race remains. For this, we need to divide the remaining laps by total laps, that is, 37 1/2 divide by 50 or 37.5 divided by 50 which will be equal to 0.74 or 3/4.
37 1/2 / 50 = 0.74 or 3/4
Hence, the right answer to the riddle is 3/4 Did you answer this riddle correctly?
YES NO
As per the total laps in the race are 50 and the driver has completed 12 1/2 laps. This means, we have to subtract 12 1/2 from the total 50 laps. This equal to 37 1/2 or 37.5
50 - 12 1/2 = 37 1/2 or 37.5
Now, we need to calculate the fractional part of the race remains. For this, we need to divide the remaining laps by total laps, that is, 37 1/2 divide by 50 or 37.5 divided by 50 which will be equal to 0.74 or 3/4.
37 1/2 / 50 = 0.74 or 3/4
Hence, the right answer to the riddle is 3/4 Did you answer this riddle correctly?
YES NO
What Flattens All Mountains Riddle
Hint:
A Boy Was 15 In 1990 Riddle
Hint:
The boy lived before Christ. Therefore, in 1995 B.C. he was 10 years old, and in 1990 he turned 15. Did you answer this riddle correctly?
YES NO
YES NO
Clock Calculator Bulb Riddle
Hint:
Find the value of one clock using the first equation. According to first equation, 9’o clock + 9’o clock + 3'o clock = 9 + 9 + 3 = 21.
Therefore; 1 Clock = 1
Using equation two, three calculators are equal to 30. Therefore, one calculator is equal to 10.
Also, the sum of numbers inside the calculator is 1 + 2 + 3 + 4 = 10.
Therefore, the value of the calculator depends on the sum of the numbers inside it.
According to equation three, 1 Bulb + 1 Bulb - 1 Bulb = 15.
Cancelling out the + and -; we get 1 Bulb with five lights = 15
.
Therefore, one bulb with one light = 3.
Bulb with four lights = 4 x 3 = 12.
The final equation is - 9’o clock + Calculator (1+2+2+4) x 3 bulbs (with four light rays each)
Translating the final equation into numbers - 9 + (1+2+2+4) x 3(12)
9 + 9 x 36 = 9 + 324 = 333.
Answer to 'Watch Calculator bulb' puzzle is 333. Did you answer this riddle correctly?
YES NO
Therefore; 1 Clock = 1
Using equation two, three calculators are equal to 30. Therefore, one calculator is equal to 10.
Also, the sum of numbers inside the calculator is 1 + 2 + 3 + 4 = 10.
Therefore, the value of the calculator depends on the sum of the numbers inside it.
According to equation three, 1 Bulb + 1 Bulb - 1 Bulb = 15.
Cancelling out the + and -; we get 1 Bulb with five lights = 15
.
Therefore, one bulb with one light = 3.
Bulb with four lights = 4 x 3 = 12.
The final equation is - 9’o clock + Calculator (1+2+2+4) x 3 bulbs (with four light rays each)
Translating the final equation into numbers - 9 + (1+2+2+4) x 3(12)
9 + 9 x 36 = 9 + 324 = 333.
Answer to 'Watch Calculator bulb' puzzle is 333. Did you answer this riddle correctly?
YES NO
I May Be Simple I May Be Complex Riddle
Hint:
12 Pills Riddle
Hint:
E = easier in "1", H = heavier in "1". 1: Weight 4:4. If they balance go to "2", if they don't balance, go to "3". 2: Balance 1:1 of the pills you didn't weight yet. Then weight one you didn't weight and one you did weight. If they balanced in the first weighing, and balanced in the second weighing, the last pill is the right one. If they balanced in the first weighing and didn't balance in the second, the one you didn't use before is the right pill. If they didn't balance at all, it's the pill you weighed twice. If they didn't balance in the first weighing, but balanced in the second, it is the first pill. 3: Weight EHH : EHH. If they balance, weight one you already weighed, with an unweighed and go to "4". If they don't balance go to "5". 4: If they balance, the one you didn't weight at all is the right pill. If they don't balance, the one you only weighed once is the right one. 5: Give away every pill that was once easier AND once heavier. You should only have EHH left. Weight H:H. If they balance, E is the right one. If the don't balance, the one which was only heavier the whole time, is the right pill. Did you answer this riddle correctly?
YES NO
YES NO
I Am A 8 Letter Word Riddle
I am kept Secret from Everyone.
My 2nd, 3rd, 4th Letter Spell an Animal.
My 4th, 5th, 6th, 7th, 8th Letter is a Weapon.
My 1st, 2nd, 8th Letter is used for Writing an Exam.
My 3rd, 4th Letters are the Same.
Who am I?
Hint:
A Woman Was In Court For Killing Her Husband Riddle
The entire jury stares at the doors waiting for waiting for this woman's husband to walk through the doors. The lawyer and the woman stare at the jury.
The lawyer concludes by saying, "See! If you were so sure she killed her husband, you wouldn't be watching that door!"
The jury immediately gave a guilty verdict. Why?
Hint:
The woman was watching the jury and not the doors because she knew that her husband wouldn't walk through them because she had killed him. If she has really missed him like she said, she would have been watching the doors. Did you answer this riddle correctly?
YES NO
YES NO
12 Islanders Teeter Totter Riddle
You must use a see-saw to figure out whose weight is different, and you may only use the see-saw 3 times. There are no scales or other weighing device on the island.
How can you find out which islander is the one that has a different weight?
Hint:
Six on one side - six on the other = one side is heavier.
Take the heavier six men, divide them into three and three (random).
Three on one side - three on the other = one side will one heavier.
Divide that three men from the heavier side side, have one on one side - one on the other.
Two results can determine which of the last three men weight is a different weight than each other.
With the last group of three men, have two men go head-to-head. The see-saw will either weight different: one weights more than the other man meaning the heavier man is the "12th man" or the see-saw will balance between the two men because they are the same weight. That means the third man standing on the sidelines by default weights more than the last two men weighted. Thus making that man on the sidelines the "12th man" that weights more than other 11.
Heavier wins 6v6; winner gets divided. Heavier wins 3v3; winner gets divided. Heavier wins 1v1 (12th man) or Equal 1v1 = third man weight more, he's the 12th man.
You could find the same results changing the process and picking from the lighter group three times. You’re only trying to find the difference in weight. Not the exact weight (more or less) of that "12th man."
Lightest 6v6; Lightest 3v3; Lightest 1v1 or Equal 1v1 = third man weight less. Did you answer this riddle correctly?
YES NO
Take the heavier six men, divide them into three and three (random).
Three on one side - three on the other = one side will one heavier.
Divide that three men from the heavier side side, have one on one side - one on the other.
Two results can determine which of the last three men weight is a different weight than each other.
With the last group of three men, have two men go head-to-head. The see-saw will either weight different: one weights more than the other man meaning the heavier man is the "12th man" or the see-saw will balance between the two men because they are the same weight. That means the third man standing on the sidelines by default weights more than the last two men weighted. Thus making that man on the sidelines the "12th man" that weights more than other 11.
Heavier wins 6v6; winner gets divided. Heavier wins 3v3; winner gets divided. Heavier wins 1v1 (12th man) or Equal 1v1 = third man weight more, he's the 12th man.
You could find the same results changing the process and picking from the lighter group three times. You’re only trying to find the difference in weight. Not the exact weight (more or less) of that "12th man."
Lightest 6v6; Lightest 3v3; Lightest 1v1 or Equal 1v1 = third man weight less. Did you answer this riddle correctly?
YES NO
I Can Be The Sun Sand And A Bird Riddle
Hint:
Pierce Ones Ears Riddle
Hint:
Post Your Hard Riddles Puns Below
Can you come up with a cool, funny or clever Hard Riddles of your own? Post it below (without the answer) to see if you can stump our users.
1. Why did the math book look sad? Because it had too many problems.
2. Why did the tomato turn red? Because it saw the salad dressing.
3. What do you call a group of cows playing instruments? A moo-sical band.
4. Why did the baker go to therapy? Because he kneaded help.
5. Why did the scarecrow win an award? Because he was outstanding in his field.
6. What do you call a cheese that isn't yours? Nacho cheese.
7. Why did the man go to the doctor with a clock in his belly? Because he wanted to know what time it was.
8. Why did the bicycle fall over? Because it was two-tired.
9. What did the grape say when it got stepped on? Nothing, it just let out a little wine.
10. Why did the chicken join a band? Because it had drumsticks.
11. Why don't scientists trust atoms? Because they make up everything.
12. Why did the cookie go to the doctor? Because it was feeling crummy.
13. What do you call a fake noodle? An impasta.
14. Why did the golfer bring an extra pair of pants? In case he got a hole in one.
15. Why did the tomato turn yellow? Because it was scared of the chef.
16. Why was the computer cold? It left its Windows open.
17. What did one wall say to the other? I'll meet you at the corner.
18. Why don't seagulls fly by the bay? Because then they'd be bagels.
19. Why did the banana go to the doctor? Because it wasn't peeling well.
20. Why was the cat afraid of the tree? Because it was afraid of getting acatia.
21. Why was the broom late? It swept in.
22. Why was the firefighter afraid of the snow? Because it put out his fire.
23. Why did the tomato blush? Because it saw the salad dressing's Caesar.
24. Why did the clock go to the gym? To work on its ticks.
25. Why did the tomato go on a cruise? It wanted to see the world and catch some rays.
26. What do you call a cow that's just given birth? De-calf-inated.
27. What did one hat say to the other? Stay calm, we've got you covered.
28. Why is a dog's nose always wet? Because it's the best way to smell.
29. Why was the math book so sad? It had too many problems.
30. Why did the grape breakdance? Because it heard it through the grapevine.
31. Why was the broom late for the cleaning party? It swept in fashionably late.
32. Why did the bird join the band? It had a high pitch voice.
33. What do you call a man with no body and just a nose? Nobody Nose.
34. Why was the math book so emotional? Because it had too many problems.
35. Why did the baker need to go to therapy? Because he kneaded some help.
36. Why did the potato go to the doctor? It was starting to feel mashed.
37. Why did the tomato go on a boat? To ketchup with its friends.
38. What do you call a man with no arms and no legs in the water? Bob.
39. Why did the computer go to the eye doctor? Because it had a virus in its sight.
40. Why did the tomato blush? Because it saw the salad dressing's Italian.
41. Why did the baker go to the beach? To get a little oven time.
42. Why did the clock lose weight? Because it went back 4 seconds.
43. Why did the tomato feel left out? It wanted to join the ketchup.
44. What did one tractor say to the other? Let's hit the hay!
45. Why did the chicken cross the playground? To get to the other slide.
46. Why did the math book cry itself to sleep? Because it had too many problems to solve.
47. Why did the soda go to the doctor? Because it was feeling a little fizzy.
48. What do you call a cow with a sense of humor? Laughing cow.
49. Why was the shirt sad? Because it was hung out to dry.
50. Why was the racecar so embarrassed? Because it couldn't get a handle on its speeds.
1. Why did the math book look sad? Because it had too many problems.
2. Why did the tomato turn red? Because it saw the salad dressing.
3. What do you call a group of cows playing instruments? A moo-sical band.
4. Why did the baker go to therapy? Because he kneaded help.
5. Why did the scarecrow win an award? Because he was outstanding in his field.
6. What do you call a cheese that isn't yours? Nacho cheese.
7. Why did the man go to the doctor with a clock in his belly? Because he wanted to know what time it was.
8. Why did the bicycle fall over? Because it was two-tired.
9. What did the grape say when it got stepped on? Nothing, it just let out a little wine.
10. Why did the chicken join a band? Because it had drumsticks.
11. Why don't scientists trust atoms? Because they make up everything.
12. Why did the cookie go to the doctor? Because it was feeling crummy.
13. What do you call a fake noodle? An impasta.
14. Why did the golfer bring an extra pair of pants? In case he got a hole in one.
15. Why did the tomato turn yellow? Because it was scared of the chef.
16. Why was the computer cold? It left its Windows open.
17. What did one wall say to the other? I'll meet you at the corner.
18. Why don't seagulls fly by the bay? Because then they'd be bagels.
19. Why did the banana go to the doctor? Because it wasn't peeling well.
20. Why was the cat afraid of the tree? Because it was afraid of getting acatia.
21. Why was the broom late? It swept in.
22. Why was the firefighter afraid of the snow? Because it put out his fire.
23. Why did the tomato blush? Because it saw the salad dressing's Caesar.
24. Why did the clock go to the gym? To work on its ticks.
25. Why did the tomato go on a cruise? It wanted to see the world and catch some rays.
26. What do you call a cow that's just given birth? De-calf-inated.
27. What did one hat say to the other? Stay calm, we've got you covered.
28. Why is a dog's nose always wet? Because it's the best way to smell.
29. Why was the math book so sad? It had too many problems.
30. Why did the grape breakdance? Because it heard it through the grapevine.
31. Why was the broom late for the cleaning party? It swept in fashionably late.
32. Why did the bird join the band? It had a high pitch voice.
33. What do you call a man with no body and just a nose? Nobody Nose.
34. Why was the math book so emotional? Because it had too many problems.
35. Why did the baker need to go to therapy? Because he kneaded some help.
36. Why did the potato go to the doctor? It was starting to feel mashed.
37. Why did the tomato go on a boat? To ketchup with its friends.
38. What do you call a man with no arms and no legs in the water? Bob.
39. Why did the computer go to the eye doctor? Because it had a virus in its sight.
40. Why did the tomato blush? Because it saw the salad dressing's Italian.
41. Why did the baker go to the beach? To get a little oven time.
42. Why did the clock lose weight? Because it went back 4 seconds.
43. Why did the tomato feel left out? It wanted to join the ketchup.
44. What did one tractor say to the other? Let's hit the hay!
45. Why did the chicken cross the playground? To get to the other slide.
46. Why did the math book cry itself to sleep? Because it had too many problems to solve.
47. Why did the soda go to the doctor? Because it was feeling a little fizzy.
48. What do you call a cow with a sense of humor? Laughing cow.
49. Why was the shirt sad? Because it was hung out to dry.
50. Why was the racecar so embarrassed? Because it couldn't get a handle on its speeds.