Trending Tags
Popular Searches
A Festive Tune Delivered By A Holiday Choir Riddles, A Man Lives On The 100th Riddles About Birds In Malayalam Riddles Answers Promise Riddles Brown And Old By Day White And Young By Night My Eyes Are Gli Have Nine Faces But No Head I Sing To The Sky But Have No Voice Im Nowhere But Everywhere Riddles Egyption Riddles If It Takes A Man One Hour To Dig A Whole 2 Meters Long 2 Meters Wide And 2 Meters Deep How Longwould It Take The Same Man To Dig A Whole 4 Meters Long 4 Meters Wide And 4 Me Riddles Lightning Riddles Me Thisa Person Wakes Up From His Night Sleep Then Got Some Cereal And Th R Riddles My Age Is Three Times Riddles The Garbage Man Quit Riddles Waffles Riddles What Kind Of Room Has N Riddles Whites A Trombones Favorite Playground Equitment Riddles Why Are Skeletons Always Riddles
Feel free to use content on this page for your website or blog, we only ask that you reference content back to us. Use the following code to link this page:
Terms · Privacy · Contact
Riddles and Answers © 2019
Ceo Riddles To Solve
Solving Ceo Riddles
Here we've provide a compiled a list of the best ceo puzzles and riddles to solve we could find.Our team works hard to help you piece fun ideas together to develop riddles based on different topics. Whether it's a class activity for school, event, scavenger hunt, puzzle assignment, your personal project or just fun in general our database serve as a tool to help you get started.
Here's a list of related tags to browse: Long Riddles Math Brain Teasers Hard Riddles Best Riddles Hard Riddles Human Body Riddles Brain Teasers Puzzle Questions Riddle Of The Day
The results compiled are acquired by taking your search "ceo" and breaking it down to search through our database for relevant content.
Browse the list below:
12 Islanders Teeter Totter Riddle
You must use a see-saw to figure out whose weight is different, and you may only use the see-saw 3 times. There are no scales or other weighing device on the island.
How can you find out which islander is the one that has a different weight?
Hint:
Six on one side - six on the other = one side is heavier.
Take the heavier six men, divide them into three and three (random).
Three on one side - three on the other = one side will one heavier.
Divide that three men from the heavier side side, have one on one side - one on the other.
Two results can determine which of the last three men weight is a different weight than each other.
With the last group of three men, have two men go head-to-head. The see-saw will either weight different: one weights more than the other man meaning the heavier man is the "12th man" or the see-saw will balance between the two men because they are the same weight. That means the third man standing on the sidelines by default weights more than the last two men weighted. Thus making that man on the sidelines the "12th man" that weights more than other 11.
Heavier wins 6v6; winner gets divided. Heavier wins 3v3; winner gets divided. Heavier wins 1v1 (12th man) or Equal 1v1 = third man weight more, he's the 12th man.
You could find the same results changing the process and picking from the lighter group three times. You’re only trying to find the difference in weight. Not the exact weight (more or less) of that "12th man."
Lightest 6v6; Lightest 3v3; Lightest 1v1 or Equal 1v1 = third man weight less. Did you answer this riddle correctly?
YES NO
Take the heavier six men, divide them into three and three (random).
Three on one side - three on the other = one side will one heavier.
Divide that three men from the heavier side side, have one on one side - one on the other.
Two results can determine which of the last three men weight is a different weight than each other.
With the last group of three men, have two men go head-to-head. The see-saw will either weight different: one weights more than the other man meaning the heavier man is the "12th man" or the see-saw will balance between the two men because they are the same weight. That means the third man standing on the sidelines by default weights more than the last two men weighted. Thus making that man on the sidelines the "12th man" that weights more than other 11.
Heavier wins 6v6; winner gets divided. Heavier wins 3v3; winner gets divided. Heavier wins 1v1 (12th man) or Equal 1v1 = third man weight more, he's the 12th man.
You could find the same results changing the process and picking from the lighter group three times. You’re only trying to find the difference in weight. Not the exact weight (more or less) of that "12th man."
Lightest 6v6; Lightest 3v3; Lightest 1v1 or Equal 1v1 = third man weight less. Did you answer this riddle correctly?
YES NO
Pierce Ones Ears Riddle
Hint:
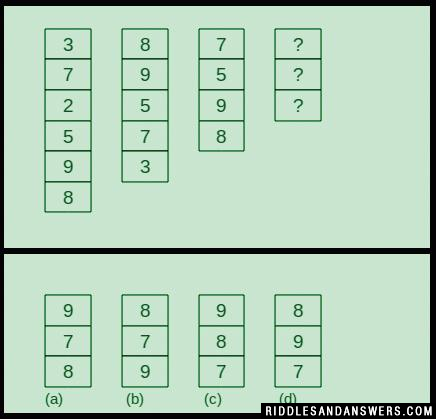
The Fourth Column Riddle
Do you know which one of the given options will take place of the fourth column?
Hint:
The correct choice will be the option 'd'.
In each succeeding row, the previous column is reversed and the lowest digits are omitted. Did you answer this riddle correctly?
YES NO
In each succeeding row, the previous column is reversed and the lowest digits are omitted. Did you answer this riddle correctly?
YES NO
Piece Of Burned Wood Riddle
Hint:
Aliens Favorite Place On A Computer Riddle
Hint:
Sweet And Bakes Riddle
I have eyes but I cant see
I have skin but I cant feel anything
I can be sweet but Im not a piece of candy
I can be baked but Im not a cake
I can be peeled but Im not a carrot
What could I be?
I have skin but I cant feel anything
I can be sweet but Im not a piece of candy
I can be baked but Im not a cake
I can be peeled but Im not a carrot
What could I be?
Hint:
Associated With Cob
Im yellow but Im not the sun
I grow in a field but Im not a sunflower
Im found on an ear but Im not a piece of jewelry
I go well with butter but Im not a slice of toast
Im associated with cob but Im not a web
What am I?
I grow in a field but Im not a sunflower
Im found on an ear but Im not a piece of jewelry
I go well with butter but Im not a slice of toast
Im associated with cob but Im not a web
What am I?
Hint:
A Piece On A Chessboard
This is in a deck of cards
And a piece on a chessboard
Shes the monarch of Britain
Who knights people with a sword
Who is she?
And a piece on a chessboard
Shes the monarch of Britain
Who knights people with a sword
Who is she?
Hint:
A 10 Foot Rope Ladder
A 10 foot rope ladder hangs over the side of a boat with the bottom rung on the surface of the water. The rungs are one foot apart, and the tide goes up at the rate of 6 inches per hour. How long will it be until three rungs are covered?
Hint:
Safe And Secure Riddle
As a whole, I am both safe and secure.
Behead me, and I become a place of meeting.
Behead me again, and I am the partner of ready.
Restore me, and I become the domain of beasts.
What am I?
Behead me, and I become a place of meeting.
Behead me again, and I am the partner of ready.
Restore me, and I become the domain of beasts.
What am I?
Hint:
Add Your Riddle Here
Have some tricky riddles of your own? Leave them below for our users to try and solve.